Grundbegriffe
Die Sprachstatistik oder quantitative Linguistik befaßt sich mit der Häufigkeit (= Frequenz) und Wahrscheinlichkeit (= Probabilität) sprachlicher Einheiten. Dies können im Prinzip Einheiten beliebiger Ebene und Art sein, also lautliche, grammatische und lexikalische Einheiten. Fundamental für den statistischen Ansatz (wie auch für manches andere) ist das Verhältnis zwischen Einheiten eines Systems und ihrem Vorkommen im Text. Man bezeichnet die Einheiten in diesen beiden Existenzweisen als Typ (engl. type) vs. Vorkommen (engl. token).
Die absolute Häufigkeit einer Einheit in einem Text ist die Anzahl ihrer Vorkommen, angegeben als ganze Zahl. Z.B. kann das Wort Bienen in einem Text von 2000 laufenden Wörtern die absolute Häufigkeit 6 haben. Die relative Häufigkeit einer Einheit ist das Verhältnis ihrer absoluten Häufigkeit zum Umfang des Textes, gemessen in Tokens derselben Ebene. Die relative Häufigkeit von Bienen in diesem Beispiel wäre als 0,003.
Im einfachsten Falle geht es um die Häufigkeit und Wahrscheinlichkeit sprachlicher Einheiten in Texten. Man kann z.B. fragen, wie häufig in einem Text abgeleitete Substantive im Verhältnis zu allen Substantiven sind. Man wird dann feststellen, daß, in Abhängigkeit vom Genre, abgeleitete Substantive verschieden häufig sind. In einem Text wie diesem z.B. sind sie relativ häufig; in einem Märchen dagegen sind sie seltener als elementare Substantive. Eine ganz andere Frage ist es, wie zahlreich abgeleitete Substantive im deutschen Lexikon sind, wiederum im Verhältnis zu allen deutschen Substantiven. Dieser Anteil ist prozentual wesentlich höher als der vorige. (Die Anzahl der Wurzeln einer Sprache ist eine kaum steigerbare Größe; aber denominale Ableitungen kann man von beliebigen Basen und beliebig komplex machen.) Folglich ist es wichtig, die Tokenfrequenz einer sprachlichen Einheit (bezogen auf ein Textkorpus) von ihrer Typfrequenz (bezogen auf das Inventar des Sprachsystems) zu unterscheiden. Statistik hat in erster Linie mit der ersteren zu tun.
Für natürliche menschliche Sprachen ist Variation auf allen Ebenen ein fundamentales Faktum. Ob eine in einem laufenden Text identifizierte Einheit tatsächlich ein Token eines bestimmten Types des Systems ist, ist eine nicht immer ganz triviale Frage, weil sie i.a. Abstraktion involviert. Z.B. ist ein in einem deutschen Text vorkommender Laut ein Token des Types [χ]. Dieser hinwiederum ist auch nur eine Instanz des Phonems /ç/. Daher kann man die Tokens als Einheiten der untersten Ebene in einer Hierarchie von Abstraktionsebenen ansehen. Und je nach Erkenntnisinteresse wird man den einzelnen vorgekommenen Laut unter [χ] oder unter /ç/ subsumieren.
Noch weit komplizierter wird die Frage, wenn es um die Zuordnung von Wortformen geht. Im vorangehenden Satz kommen zwei Tokens der Form die vor. Wenn wir uns aber nicht für Femininum oder Singular, sondern für den definiten Artikel interessieren, werden wir sie (neben der, deren usw.) als Vorkommen von diesem klassifizieren. Die Lemmatisierung ist also ebenfalls ein Schritt in dieser Hierarchie von Abstraktionsebenen. Bereits diese Beispiele genügen, um zu zeigen, daß man die Ebene der gewöhnlichen linguistischen Analyse bei der Formalisierung nicht überspringen kann und daß die Präzision der letzteren nur so weit reicht wie die Qualität der Analyse, auf der sie basiert. Vollends absurd würde diese methodologische Spannung werden, wenn man Statistik von semantischen Elementen, z.B. Bedeutungskomponenten, in Texten machen wollte. Die Sprachstatistik hält sich allermeist an solche Einheiten, die mechanisch in Texten identifizierbar sind.
Nimmt man die statistische Perspektive ein, so treten an die Stelle von Ja/Nein-Entscheidungen Wahrscheinlichkeiten, z.B. die Wahrscheinlichkeit, mit der ein Wort auftritt oder mit der eine Regel angewandt wird. Solange man nur die Vorkommen von Einheiten in einer bestimmten Stichprobe auszählt, erhält man deren (absolute oder relative) Häufigkeit. Die Wahrscheinlichkeit einer Einheit dagegen ist ein Wert, den man auf der Basis der relativen Häufigkeit errechnet. Dazu muß man mehrere Stichproben aus derselben Grundgesamtheit entnehmen und aus deren Standardabweichungen den Standardfehler berechnen. Die Wahrscheinlichkeit einer Einheit ist dann, grob gesprochen, ihre relative Häufigkeit unter Berücksichtigung des Standardfehlers. Für die Zwecke dieser Einführung werden wir in der folgenden Darstellung den Unterschied zwischen relativer Häufigkeit und Wahrscheinlichkeit vernachlässigen.
Die relative Häufigkeit ist, wie oben dargestellt, der Quotient aus der Anzahl der Tokens eines bestimmten Types und der Anzahl aller Tokens derselben Ebene (Kategorie), also dem Umfang der Grundgesamtheit (d.h. im linguistischen Falle, des Korpus). Dies ist also eine Realzahl, die Werte zwischen 0 und 1 annimmt. Dasselbe gilt für die Wahrscheinlichkeit pu einer Einheit u: Sie ist 1, wenn das Korpus ausschließlich aus Tokens von u besteht, normalerweise aber wesentlich niedriger.
Die Wahrscheinlichkeit, daß in einer Sequenz von Einheiten einer bestimmten Art eine bestimmte Einheit auftritt, hängt im Falle sprachlicher Einheiten vom Kontext ab. Z.B. liegt die Wahrscheinlichkeit des Wortes ab in einem deutschen Text etwa bei 0,0003 (also bei 3 Vorkommen auf 10.000 laufende Wörter). Die Wahrscheinlichkeit, daß das Wort am Ende des ersten Satzes dieses Absatzes ab ist, liegt jedoch fast bei 1,0. Und andererseits liegt die Wahrscheinlichkeit, daß das Wort nach bei im vorigen Satz ab ist, fast bei Null. Die Wahrscheinlichkeit einer Einheit in Abhängigkeit von den Einheiten, die in der Sequenz bis dahin aufgetreten sind, ist ihre bedingte Wahrscheinlichkeit. Die bedingte Wahrscheinlichkeit sprachlicher Einheiten hat offensichtlich mit den grammatischen Konstruktionen zu tun, in denen sie auftreten. Für einen Computer ist es allerdings relativ schwierig, eine grammatische Konstruktion zu erkennen, dagegen sehr einfach, bedingte Wahrscheinlichkeiten auszuwerten. Daher spielen diese in der Sprachinformatik eine große Rolle.
Auf allen Gebieten der Sprachwissenschaft ist Quantifikation möglich:
- Quantitative Phonologie befaßt sich mit der Wahrscheinlichkeit phonologischer Einheiten, z.B. Phonen oder Silben oder Konsonantengruppen, in Texten oder in Lexemen.
- Quantitative Morphologie befaßtn sich mit der Wahrscheinlichkeit morphologischer Einheiten in Texten bzw. in syntaktischen Einheiten. Eine einschlägige Frage ist z.B., aus wievielen Morphen durchschnittlich eine Wortform besteht.
- Quantitative Sprachtypologie konzipiert die Unterschiede im Sprachbau so, daß sie gemessen werden können.
Wir befassen uns im folgenden mit einer der wichtigsten Anwendungen der Sprachstatistik, den Frequenzwörterbüchern (oder Häufigkeitswörterbüchern). Die sprachlichen Einheiten, um die es dabei geht, sind in erster Linie Wortformen. Die meisten Frequenzwörterbücher unterscheiden sich in der Tat von gewöhnlichen Wörterbüchern darin, daß sie auf dieser Abstraktionsstufe stehenbleiben, während der Gegenstand der letzteren i.a. Lexeme sind.
Informationstheorie
Würde man die Wahrscheinlichkeit, mit der eine bestimmte sprachliche Einheit auftritt, kennen, so würde man sie mit entsprechender Sicherheit in Texten erwarten können. Das Auftreten einer sprachlichen Einheit, deren Wahrscheinlichkeit = 1 ist, kann man mit 100%iger Sicherheit erwarten. Eine solche Einheit hat keinerlei Neuigkeitswert; dadurch, daß sie auftritt, erfährt man nichts, was man nicht schon wußte. Dadurch, daß man z.B. am Ende jenes oben angeführten Satzes (Sektion 1, Absatz 8, Satz 1) ab liest, bekommt man keinerlei Information; es ist dort vollständig redundant. Und andererseits: je weniger man ein bestimmtes Signal erwarten konnte, desto mehr Information erhält man durch es. Die Informationstheorie hat deshalb einen Begriff der Informationsmenge eines Signals entwickelt, der an dessen Überraschungswert gekoppelt ist. Und dieser steht nach dem soeben Gesagten im umgekehrten Verhältnis zur Wahrscheinlichkeit des Signals. Im folgenden wird dieser Informationsbegriff erläutert. Er ist jedoch leichter anhand der Typfrequenz als anhand der Tokenfrequenz zu verstehen. Daher betrachten wir zunächst die Informationsmenge einer sprachlichen Einheit als das Maß der Wahlmöglichkeit bei seiner Selektion. Dieses wiederum werden wir bestimmen als die Anzahl der Entscheidungen, die bei seiner Selektion zu fällen sind.
Wir gehen aus von einem Inventar von n Elementen, die alle voneinander verschieden sind, also den Charakter von Types haben. In folgendem Schema ist n = 8.
Schema: Auswahl aus gleich wahrscheinlichen Elementen
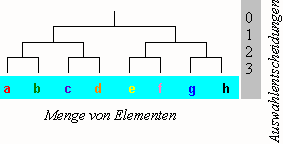
Wie der Entscheidungsbaum verdeutlicht, benötigt man hier drei binäre Entscheidungen, um ein Element zu identifizieren. Gegeben ein Inventar von n verschiedenen Elementen (deren Wahrscheinlichkeit nicht berücksichtigt wird), so ist die Anzahl der zur Identifikation eines Elements u benötigten binären Entscheidungen:
| G1. | Iu = ld n1 |
Iu ist die Informationsmenge des Elements u, gemessen in Bits. Eine binäre Entscheidung ist ein Bit, und dies ist gleichzeitig die minimale Informationsmenge und deren kleinste Maßeinheit. Wie man sieht, gilt, daß je größer n wird, desto größer auch I wird.
In einem zweiten Ansatz beziehen wir die Berechnung jetzt nicht auf Types eines Inventars, sondern auf die Tokens, die in einem Text vorkommen. Sei n die betrachtete Gesamtzahl von Vorkommen von Elementen, u eins dieser Elemente und x die Anzahl der Vorkommen von u (als Teil von n). Dann ist die relative Häufigkeit von u:
| G2. | Fu = x/n |
Wie angekündigt, nehmen wir dies, mit einiger Vereinfachung, als Wahrscheinlichkeit von u. Daher:
| G3. | pu = x/n |
Wenn also alle Elemente gleich wahrscheinlich sind, hat jedes die Wahrscheinlichkeit
| G4. | pu = 1/n |
Wenn z.B. ein Element doppelt so häufig ist wie die anderen, ist seine Wahrscheinlichkeit 2/n, bei acht Elementen also 2/8 = 1/4 = 0,25.
Betrachten wir jetzt wieder die Anzahl von Entscheidungen, die jemand trifft, um ein Element aus einer Menge von verschieden wahrscheinlichen Elementen auszuwählen. In folgendem Schema gibt es insgesamt 8 Tokens, davon zwei von c und vier von d.
Schema: Auswahl aus verschieden wahrscheinlichen Elementen
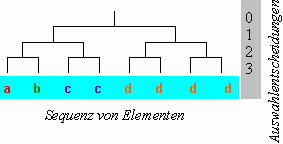
Wenn wir nun die Informationsmenge, statt wie vorhin auf die Anzahl n, auf die Wahrscheinlichkeit eines Elements beziehen, können wir einen Begriff der Informationsmenge eines Elements der Wahrscheinlichkeit pu = xu/n zunächst induktiv erschließen, indem wir eine Formel für die in diesem Schaubild vorliegenden Bitwerte suchen. Anhand der Beispiele beobachten wir folgenden Zusammenhang zwischen der Wahrscheinlichkeit eines Elements und der Anzahl binärer Entscheidungen, die zu seiner Identifikation nötig sind:
- Die am wenigsten wahrscheinlichen Elemente –
aundb– kommen nur einmal vor. Ihre Wahrscheinlichkeit ist also1/n. Sie haben die höchste Informationsmenge. Gemäß obigem Schema sind es3 Bits. - Die Anzahl der notwendigen Entscheidungen für das Element
cmit der Wahrscheinlichkeit1/4ist2 Bits, für das Elementdmit der Wahrscheinlichkeit1/2ist sie1 Bit. - Allgemein: Elemente mit höherer Wahrscheinlichkeit haben niedrigere Informationsmenge.
Die folgende Gleichung repräsentiert diese Beziehung:
| G5. | Iu = ld n - ld x |
Immer noch intuitiv-abduktiv betrachtet und mit G1 verglichen, stellt G5 dar, daß (absolute) Häufigkeit dem Informationsgehalt abträglich ist. Z.B. für das Element c in obiger Sequenz:
| G6. | Ic | = ld 8 - ld 2 |
| = 3 - 1 | ||
| = 2 |
Wenn wir die Berechnung von I auf Elemente mit beliebiger Wahrscheinlichkeit verallgemeinern wollen, so brauchen wir in G5 nur noch p statt x und n einzusetzen:
| G6. | Iu | = - (ld x - ld n) | (Umformung von G5) |
| = - ld x/n | |||
| = - ld p |
Die Korrelation ist also wie folgt: Die Informationsmenge I eines Elements u eines Zeichensystems ist der negative Logarithmus zur Basis 2 der Wahrscheinlichkeit pu:
| G/. | Iu = -log2 pu Bits |
Fazit: Die Informationsmenge eines Signals ist desto größer, je weniger wahrscheinlich/vorhersehbar es ist.
Informationsmenge und Bedeutungsspezifizität
Als nächstes verschaffen wir uns einen anschaulichen Eindruck von den Größenordnungen, die reale Informationswerte von sprachlichen Einheiten annehmen. Dazu stehen eine Reihe von Frequenzwörterbüchern des Deutschen zur Verfügung. Wir ziehen zunächst Ruoff 1981 heran, wo 500.000 laufende Wortformen ausgezählt wurden. Die folgende Tabelle gibt ein paar Beispiele; die zweite Spalte gibt die absolute Häufigkeit in Ruoff 1981 wieder, die letzte zeigt die Informationsmenge in Bit.
| Beispiel | Häufigkeit | Wahrscheinlichkeit | Inf.menge |
|---|---|---|---|
| und | 22.896 | 0,046 | 4,4 |
| so | 2.271 | 0,0045 | 7,8 |
| Hof | 229 | 0,00046 | 11,1 |
| Lehrerin | 23 | 0,000046 | 14,4 |
Da die Informationsmenge nicht linear, sondern logarithmisch wächst, wenn die Wahrscheinlichkeit sinkt, nimmt sie selbst bei sehr seltenen Wörtern keine riesigen Werte an. Aus dieser Stichprobe kann man folgendes verallgemeinern:
- Die häufigsten Wörter einer Sprache sind die grammatischen Wörter (Formative). Die Häufigkeit korreliert ziemlich genau mit dem Grade ihrer Grammatikalisierung. Einer der Parameter der Grammatikalisierung ist ja die Obligatorietät. In dem Maße, in dem eine sprachliche Einheit obligatorisch wird, wird sie notwendigerweise wahrscheinlicher.
- Die Informationsmenge von Wörtern nimmt Werte in der Größenordnung zwischen 4 und 25 Bits an.
- Repräsentiert man die Bedeutung eines Wortes (seine Intension) als eine Menge von semantischen Merkmalen oder von elementaren Propositionen, so liegt deren Anzahl typischerweise in eben derselben Größenordnung. Man kann sich also, mit starker Vereinfachung, das semantische Merkmal als das semantische Gegenstück des Bits vorstellen. Dann entspricht die Informationsmenge eines Ausdrucks wie im vorigen Abschnitt definiert seiner semantischen Spezifizität, repräsentiert als eine Menge elementarer Propositionen.2
Angenommen, wir würden die semantische Analyse so weit formalisieren, daß paradigmatische semantische Relationen zwischen Zeichen in regelmäßiger Weise durch die Zusammensetzung ihrer semantischen Repräsentationen aus semantischen Merkmalen abgebildet würden. Dann würde sich aus dem Gesagten folgende Hypothese ergeben: Gegeben zwei beliebige Ausdrücke (z.B. Wörter) A1 und A2, die sich dadurch unterscheiden, daß A2 ein semantisches Merkmal mehr hat als A1. Dann ist die Informationsmenge von A2 um einen Wert größer als die von A1, der je nach Merkmal um 1 Bit liegt. Beispiele von Paaren, die die Bedingung erfüllen, erscheinen in folgender Tabelle. Die Häufigkeiten sind diesmal Kaeding 1897 entnommen, einem Frequenzwörterbuch, das auf einem Korpus von 10.910.777 laufenden Wortformen basiert.3
| Beispiel | Häufigkeit | Wahrscheinlichkeit | Informationsmenge |
|---|---|---|---|
| Lehrer | 1.252 | 0,0001147 | 13,1 |
| Lehrerin | 77 | 0,0000071 | 17,1 |
| Student | 102 | 0,0000093 | 16,7 |
| Studentin | <10 | <0,0000009 | >20,1 |
| Hund | 205 | 0,0000188 | 15,7 |
| Hündin | <10 | <0,0000009 | >20,1 |
| Katze | 65 | 0,0000060 | 17,4 |
| Kater | 28 | 0,0000026 | 18,6 |
| Gans | 20 | 0,0000018 | 19,1 |
| Gänserich | <10 | <0,0000009 | >20,1 |
| arbeite ∪ arbeitet | 55+258 | 0,0000287 | 15,1 |
| arbeitete | 197 | 0,0000181 | 15,8 |
| liebe ∪ liebt | <6.665+598 | <0,0006657 | >10,6 |
| liebte | 432 | 0,0000396 | 14,6 |
| nahmst | 19 | 0,0000017 | 19,1 |
| nahmt | 4 | 0,0000004 | 21,4 |
| nimm | 357 | 0,0000327 | 14,9 |
| nehmt | 157 | 0,0000144 | 16,1 |
- In der ersten Teilmenge von Beispielen geht es um das Merkmal [weiblich], welches bei den auf -in abgeleiteten Wörtern gegenüber ihren Basen hinzukommt. Wie man sieht, haben die ersteren durchschnittlich eine um 4 Bit höhere Informationsmenge.
- In der zweiten Teilmenge geht es um das Merkmal [männlich], welches bei Kater und Gänserich gegenüber ihren Basen dazukommt. Wie man sieht, haben die ersteren durchschnittlich eine um 1,5 Bit höhere Informationsmenge.
- In der dritten Teilmenge geht es um das Merkmal [Präteritum], welches bei den mit -t suffigierten Verbformen gegenüber den präsentischen hinzukommt. Wie man sieht, haben die ersteren eine höhere Informationsmenge.4
- In der letzten Teilmenge schließlich geht es um das Merkmal [Plural], welches bei den mit -t suffigierten Formen gegenüber den singularischen hinzukommt. Wie man sieht, haben die ersteren eine durchschnittlich um 1,3 Bit höhere Informationsmenge.5
Gleichzeitig ist dies ein Beispiel mathematischer Linguistik, das eine praktische Anwendung hat: So kann man z.B. ein Frequenzwörterbuch dazu benutzen, um für einen Sprachkurs den Lernerwortschatz schrittweise strukturiert aufzubauen.
1 “I von u ist gleich dem Logarithmus dualis von n.” Der Logarithmus dualis (d.h. log2, Logarithmus zur Basis 2) zu n ist die Zahl, mit der man 2 potenzieren muß, um n zu erhalten.
2 Ein komplexer Ausdruck, der mehr als eine Proposition umfaßt, ist allerdings nicht einfach eine Menge von Propositionen. Vielmehr sind die einzelnen Propositionen durch aussagenlogische Junktoren wie ‘und’ (konjunktiv) und ‘oder’ (disjunktiv) aufeinander bezogen. Die semantische Spezifizität wächst nur durch konjunktiv verbundene Propositionen; disjunktiv verbundene dagegen sind ihr abträglich (sie erhöhen die Polysemie). Weiteres dazu auf der Seite über Information.
3 Tatsächlich konsultiert wurde die Ausgabe von Meier 1964, wo die meisten Wortformen, die bei Kaeding weniger als zehnmal vorkamen, unterdrückt sind.
4 Im Präteritum herrscht Synkretismus zwischen der 1. und der 3. Ps; daher wurde im Präsens die Vereinigungsmenge der Vorkommen der entsprechenden Formen gebildet.– Die Zahl der Vorkommen von liebe ist so hoch, weil in Kaeding 1897 <liebe> und <Liebe> nicht auseinandergehalten werden.
5 Die imperativische Form nimm statt der indikativischen nimmst ist ein Fehler in dieser Stichprobe.
Literatur
Kaeding, Friedrich Wilhelm (ed.) 1897, Häufigkeitswörterbuch der deutschen Sprache. Teil 1: Wort- und Silbenzählungen. Steglitz bei Berlin: Selbstverlag.
Lehmann, Christian 1978, "On measuring semantic complexity. A contribution to a rapprochement of semantics and statistical linguistics." Georgetown University Papers on Languages and Linguistics 14:83-120.  ]
]
Meier, Helmut 1964, Deutsche Sprachstatistik. Hildesheim: G. Olms.
Ruoff, Arno 1981, Häufigkeitsworterbuch gesprochener Sprache, gesondert nach Wortarten alphabetisch, rücklaufig alphabetisch und nach Häufigkeit geordnet. Tübingen: M. Niemeyer (Idiomatica, 8).